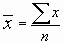
What is the best way to measure water volumes? Three factors to consider when answering this question are precision, accuracy, and convenience. No single method is likely to be best on all three. This simple lab will give you some experience on which to base your decision about what method to use when measuring water volumes.
You will compare three measuring devices at three different volumes. To measure one milliliter (mL) and ten milliliters, you will use a graduated cylinder, a pipet and a buret. To measure one hundred milliliters, you will use a graduated cylinder, a beaker and a volumetric flask. To check on the precision and accuracy of these measurements, you will use an analytical balance. In addition to the volume measuring devices and a balance, you will need various pieces of glassware and a thermometer.
Obtain a tare mass on a plastic weigh boat. Add using a pipet, add one milliliter of deionized water to the boat and obtain a gross mass. Check the temperature of the water that you are using for these measurements. Be sure that you have a reliable tare mass before each addition of more water to the boat.
Repeat the measurement until you have five useable data points. Record all the data in your laboratory observation notebook. Actual measurements and observations should be recorded on the right hand page. Calculations and comments can be entered on the facing left hand page. This data will not necessarily be turned in, but it should be available for inspection on request. If someone else makes the measurements, their name or initials should be noted as well.
The actual volume of water added to the boat can be assumed to be equal to the mass of water added divided by the density of water at the observed temperature. The volumes you obtain by calculation from the mass can be compared with the desired "true" value (ie, the volume you were trying to measure out--1 mL, 10 mL or 100 mL).
Note: You may be asked to check the operation of the balance before each set of weighings using a reference weight. Record the value you obtain for each reference check on the left side of your notebook, opposite the experimental measurements.
Repeat the procedure using a buret to measure one milliliter into the boat. Again obtain five data points. Likewise, obtain five data points by dispensing one milliliter from a graduated cylinder. Alternatively, you can measure one milliliter with more than one size pipet (eg, use a 1 mL and a 5 mL).
Repeat the measurements dispensing ten milliliters and one hundred milliliters.
For each data point, calculate a true volume of water measured out. This value is calculated by subtracting the tare mass from the gross and dividing the difference by the density of water. When you have finished making measurements and calculations, you should have nine sets of five volumes. Three sets of volumes should be close to 1.0 mL, three close to 10 mL and three close to 100 milliliters. For each set, calculate an average volume, a standard deviation and a coefficient of variation. The accuracy of each set of measurements can be checked by comparing the means with the nominal values (1, 10 or 100 mL). The calculations can be done on a spreadsheet or a hand calculator that has statistical functions (such as a TI 83 or TI 86). If you use a spreadsheet, you can also print out nice looking tables. The functions in Excel are AVERAGE to calculate the mean and STDEV to calculate the standard deviation.
Present these results (individual volumes and descriptive statistics) in three tables (one for 1.0 mL, etc).
For each volume,
You should use an appropriate number of significant figures for your tabulated results.
The precision of a repeated measurement is determined by how close together values are. This is quantified by the coefficient of variation. The accuracy is determined by how close measured values are to a known true value. This is expressed by the percent recovery. A precise and accurate measurement has a low CV and a percent recovery close to 100 percent.
Bonus: If your temperature measurement(s) were off by one full degree, to what extent would it affect the precision and/or accuracy of these results?
For n values of x, you can calculate as follows:
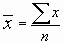
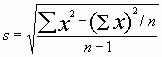
Note: if you calculate this by hand, you need to retain a large number of decimal places in the intermediate values.
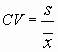
For a measured value (or mean measured value) xm and a known true value xtv, calculate the percent recovery (%R) as follows:

In this case, you will be using an xm equal to the mean of the volumes calculated from the masses and an xtv equal to the volume you thought you were measuring out (eg, 1 mL). In a case such as this, the xtv is sometimes called a "nominal value" rather than a true value.
The relative percent error (RPE) is the percent recovery minus 100 percent (eg, for a %R of 103% the RPE = 3%). The closer the RPE is to zero, the more accurate the measurement.
Note that the standard deviation or coefficient of variation tells us how much repeated measurements are likely to vary. When values are selected from a group that has a normal distribution (ie, a bell curve), most of them (68%) will fall within one standard deviation of the mean.
It is customary to record all the digits of a digital readout or one more digit than is marked on an analog scale. However, the magnitude of the CV of a series of measurements gives us a more realistic indication of what number of significant figures is appropriate to use for that measurement. If the CV is ~0.1, we would expect most measurements to fall within 10 percent of the mean so we would record our measurement to two significant fiqures. If the CV is ~0.01, we would use three and so forth.
"Add a volume of deionized water to the boat using the device being assessed. Try to dispense as close to the nominal volume (1 mL, 10 mL or 100 mL) as you can."