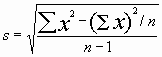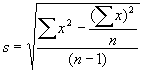Important Concepts of Statistics and Probability
ENV* K245 Water Resources Engineering home
Note: Precipitation homework, due 10/5: McCuen, Hydrologic Analysis and Design, Chapter 4, Problems 4.2, 4.6, 4.7, 4.9, 4.10, 4.15
Descriptive statistics
- These summarize a set of observations
- In general these might be:
- Heights of a group of people
- Test scores
- Size variation on a manufactured part
- In hydrology some examples are:
- Annual maximum 24 hour rainfall
- Lowest flow in a river within a ten day period of each year
- Number of days between rainfall events
- Commonly used statistics include:
- Measures of central tendency—These say where the middle of a group of observations is.
- mean = average (aka m or x-bar)
- Add up the values and divide by the number of values:
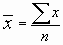
- median = the middle value
- mode = the most common value
- Measures of variability—These tell us how spread out a set of numbers are.
- standard deviation = the square root of the average squared difference between each number and the mean
- This difference can be manipulated algebraically to give a form that is easier to calculate:
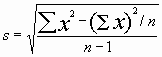
- range = the difference between the highest and lowest numbers
|
4 3
5 4
6 5
6 6
6 2
|
mean: 4.7
median:5
mode: 6
sd: 1.4
range: 4
|
Inferential statistics
- These allow us to make inferences beyond the observations
- For example, suppose that within a particular group of 100 children, girls scored higher than boys on a particular test. Does that mean that it is likely that another group of girls will also score higher than another group of boys?
- Hypothesis testing
- From a given set of numbers (eg, scores) we can determine the probability that a certain distribution occurred by chance.
- If the probability is less than some value, say 5% or 1%, than we say that the finding is statistically significant.
- I don’t think we will use inferential statistics in this class, but examples include t-value and F-value.
Samples vs populations
Random Variables
- A random variable is a series of numbers that we can consider one at a time.
- For those of you who like symbols, note that the random variable is often abbreviated with a capital letter, X, while any particular value is abbreviated with lowercase letter, often subscripted, x1.
- The set of all possible values for the random variable is a population.
- A set of some particular values is a sample, (x1, x2, x3,…,xn).
- We’ve already considered some examples.
- Height is random variable and so is maximum annual 24-hour rainfall.
Distribution
- A distribution is a mathematical description of how values are distributed in a population.
- There are several well known distributions, including:
- The uniform distribution—such as the distribution of values shown on the face of a single die
- All values are equally likely, e.g., 1 through 6
- The binomial distribution—such as the numbers of consecutive heads or consecutive tails in a set of coin tosses
- The normal distribution, also called the bell curve
- Many random variables are assumed to be distributed according to the normal distribution.
- The probability of any value of a normally distributed random variable can be predicted using a table of z values, Excel, or other techniques.
Frequency Analysis
- we often speak of the 2 year storm or the 10 year storm or the 25 year flood etc
- the T-year storm or flood is the storm or flood of intensity that will on the average be met or exceeded once in T years
- we can also talk about an T-year drought or low QN which would be the conditions equaled or gone less than on the average once in T years
- T is called the recurrence interval or return period
- these things are surprisingly easy to calculate from a series of yearly data
- generally speaking we want at least 10 years of data or T/2 whichever is greater (eg, we can estimate the 100 year storm from 50 years of data)
- the general idea is to draw up a plot of intensity versus frequency or probability (on probability paper) and read off the intensity that corresponds to 1/T
- to do this:
rank the n items of data from highest to lowest (if we want a rare high event) or lowest to highest), assign a number m corresponding to the rank
calculate a probability P that the item at rank m will be exceeded:
Hazen’s formula gives:
Fa = (2n-1)/2y; the third highest item of ten would have P = (2*3-1)/(2*10) = 0.25
[or sometimes we might use P = n/(y+1) so for example the 3rd highest item of 10 would be P = 3/(10+1) = 0.27]
- we are assuming that we’re looking for rare high values
- plot each item above its probability
- sketch the line that fits the points and find the rainfall, etc, that corresponds to P=1/T
Given this data for maximum flow at Babbling Brook during the month of August, what is the 20-year storm?
|
Year
|
QH (cfs)
|
|
1963
|
490
|
|
1964
|
440
|
|
1965
|
460
|
|
1966
|
550
|
|
1967
|
430
|
|
1968
|
360
|
|
1969
|
510
|
|
1970
|
410
|
|
1971
|
390
|
|
1972
|
470
|
Show graph
- a very similar thing could be done mathematically:
- find the mean and standard deviation of the items:
mean = X = å
x/n
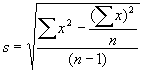
- look up in a table of z values (ie, the normal distribution) the z value corresponding to P=1/T, call this value K (the z value for the
entry=0.5-P)
- our T-year event is then given by:
xT = X + Ks
Homework exercise: What is the 50-year maximum precipitation for the month of September at the Norwich Public Utility Station? Use the monthly data in the link below. Plot either the original values on log-prob paper or the log of the values on arith-prob paper.
Top of page
ENV* K245 Water Resources Engineering home
Environmental Engineering Technology home
Anthony G Benoit
abenoit@trcc.commnet.edu
(860) 885-2386
Revised
![]()
![]()